刚写完 关于区块链的一点点思考 脑子里就回想起之前关于鱼竿的的文章还没写完,然后想起该写鱼竿的硬度了。玩过鱼竿的都知道,碳布吨位越高鱼竿越硬,同时也越脆。那么假设鱼竿的硬度为y轴,脆度为x轴,他们之间的关系会不会呈现出一种有规律的形状呢?比如下面这个:

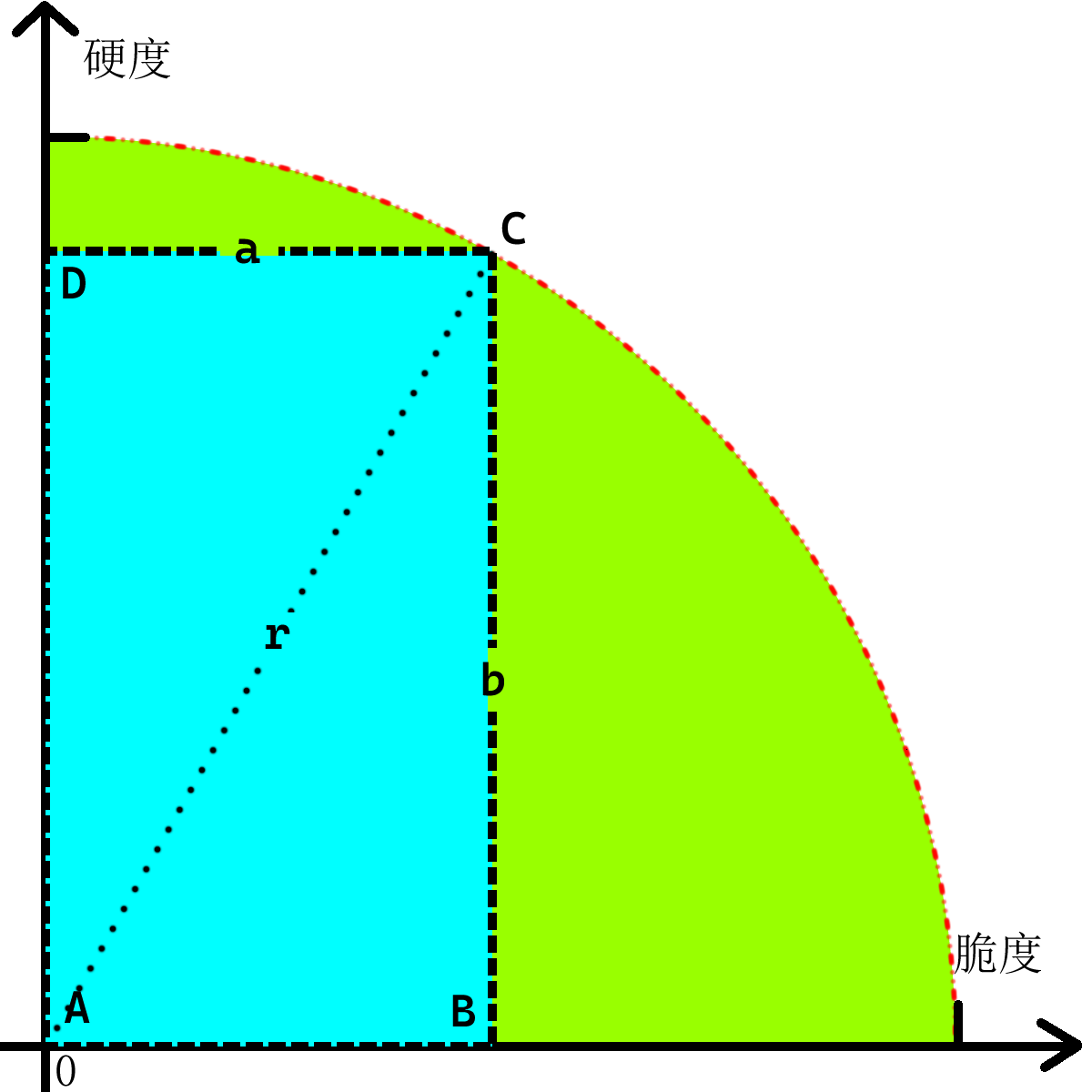
答案肯定不是这样的,图中这种情况太过于理想了,但是不管了,我看到这个图就想起了一个题:假使黄色区域是以原点为圆心,r 为半径的扇形。那么在这个扇形中画矩形,能够画出的最大的矩形面积是多少?这个题想了很久没有想出来,后面慢慢想。现在给这个矩形加个条件,矩形的一个角的顶点与原点重合,两条边分别与x轴和y轴重合,如下图所示:

四边形ABCD为矩形,A点与原点重合,B点在横轴上,C点落在扇形的弧形边上。扇形的半径为r,四边形ABCD的最大面积和最大周长分别是多少?
解
- 最大面积求解
设:矩形AB边长为a, BC边长为b, 面积为S
所以有 S = ab
由图中可以得知,矩形的对角线长度就是扇形半径长,为r
从勾股定理可以得到等式:a² + b² = r²
假设:b = a + c
则:a² + (a + c)² = r²
得:a² + a² + 2ac + c² = r²
得:2(a² + ac) = r² - c²
又因 ab = a(a + c) = a² + ac
所以 S = ab = (r² - c²) / 2
要使 S 最大,c²要
因此c²为0时, 矩形面积S得最大值 r²/2
- 最大周长求解
同设:矩形AB边长为a, BC边长为b, 周长为C
所以 C = 2(a + b)
由图中可以得知,矩形的对角线长度就是扇形半径长,为r
从勾股定理可以得到等式:a² + b² = r²
所以有: (a + b)² = a² + 2ab + b² = r² + 2ab
所以: C = 2(a + b) = 2 \sqrt[2]{( r² + 2ab)}
又因为 ab 的 最大值为 r² / 2
矩形周长C的最大值为 2r \sqrt[2]{2}